
Now for some maths
I now have to introduce you to some equations. I’m going to try to keep the maths down to an absolute minimum but it will be useful for you to learn some notation. I’ll feed you the maths little by little and introduce new concepts when we get to the relevant sections. This way I hope your mind can absorb all the ideas a little more comfortably and you'll be able to see how the maths are put to work at each stage in the development of a neural net.
A neuron can have any number of inputs from one to n, where n is the total number of inputs. The inputs may be represented therefore as x1, x2, x3… xn. And the corresponding weights for the inputs as w1, w2, w3… wn. Now, the summation of the weights multiplied by the inputs we talked about above can be written as x1w1 + x2w2 + x3w3 …. + xnwn, which I hope you remember is the activation value. So…
a = x1w1+x2w2+x3w3... +xnwn
Fortunately there is a quick way of writing this down which uses the Greek capital letter sigma S, which is the symbol used by mathematicians to represent summation.

Maybe just to clarify what this means I should write it out in code. Assuming an array of inputs and weights are already initialized as x[n] and w[n] then:
double activation = 0;
for (int i=0; i<n; i++)
{
activation += x[i] * w[i];
}
Got it? Now remember that if the activation > threshold we output a 1 and if activation < threshold we output a 0.
Let me illustrate everything I've shown you so far with a diagram.
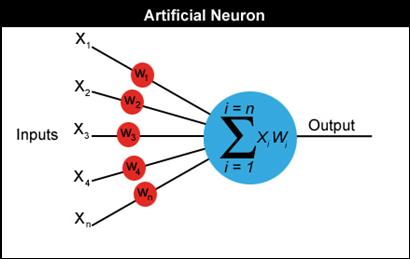
Please ensure that you understand exactly how to calculate the activation value before you move on.